ГлавнаяОлимпиады по математикеОлимпиада — Олимпиада 2х2

Подготовка к Олимпиаде МИРЭА
(творческая лаборатория 2х2)

логотип олимпиады 2х2

Творческая лаборатория «Дважды два» регулярно проводит математические соревнования для школьников 1-8 классов. Для учащихся начальной школы ежегодно проводится олимпиада 2х2 по математике МИРЭА. В 2018 году олимпиада будет проводиться 11 февраля. В ней могут участвовать ученики 1, 2, 3 и 4 классов.

Чтобы принять участие в олимпиаде, нужна серьезная подготовка. Обращайтесь за помощью к профессиональному репетитору. Связаться с преподавателем по олимпиадной математике 2х2 можно по телефону: +7 (903) 015-01-10 или электронной почте: math@tutordt.ru

 

Особенности заданий

Задачи, которые дают на конкурсе, нестандартные. Ребенку нужно проявить творческие и креативные способности, чтобы найти правильное решение. Примеры задач олимпиады «Дважды два» по математике прошлых лет приведены ниже. Они помогут оценить возможности вашего ребенка, а также дадут примерное представление о заданиях, которые дети выполняют на конкурсе.

История олимпиады

олимпиада МИРЭАИстория этой олимпиады началась в 1996 году. Именно тогда впервые возникла идея провести соревнование для участников математического кружка. Основной целью этого мероприятия было дать возможность школьникам начальных классов проявить свои творческие и интеллектуальные способности в индивидуальной работе. В первой олимпиаде участвовало всего 15 человек.

С каждым годом популярность конкурса росла, как и количество его участников. Происходили изменения в правилах и организации. География олимпиады стала намного шире: теперь в соревновании участвуют не только школьники Москвы, но и других российских городов и даже стран.

Математическая олимпиада 2х2 для школьников младших классов в 2018 году пройдет 11 февраля. Регистрироваться и подавать заявки необходимо заранее, на официальном сайте студии «Дважды два» — https://olimpiada2x2.ru/. Обработка результатов занимает больше месяца. Подведение итогов пройдет 1 апреля 2018 года.

Вариант XXI олимпиады младших школьников (2017 год)

№1. Имеются карточки с числами от 1 до 9. Расположите их в ряд так, чтобы никакие три подряд идущие карточки не лежали ни по убыванию, ни по возрастанию чисел, написанных на них.

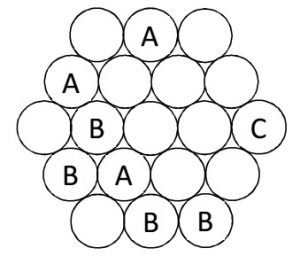
№2. Расставьте в кружках буквы А, В и С так, чтобы не было равносторонних треугольников с тремя одинаковыми буквами в вершинах.

подготовка в олимпиаде 2х2

№3. В городе есть станции метро – Альфа, Бета, Гамильтон, Дельта, Лямбда, Эпсилон, Икс и Зета. Известно, что между двумя станциями без пересадок ходит поезд, если количество букв в названиях этих станций имеют разную четность. Федя хочет проехать как можно более длинный путь, не посещая никакую станцию дважды, причем так, чтобы название каждой следующей станции было длинней предыдущей. Какой длины будет этот путь? Ответ объясните.

№4. Планета Железяка делает оборот вокруг своей оси за 5 железякских часов. А планета Каменюка делает один оборот вокруг своей оси за 6 каменюкских часов. Космический корабль летит от планеты Железяка до планеты Каменюка 20 железякских часов, а обратно 25 каменюкских часов. Какая планета вращается вокруг своей оси быстрее. Ответ объясните.

№5. Дома вдоль единственной улицы в Цветочном городе решили пронумеровать, для чего изготовили таблички с цифрами. Оказалось, что табличек с цифрой 1 потребовалось на 12 штук больше, чем табличек с цифрой 0. Какое наименьшее количество домов может быть на этой улице? Ответ объясните.

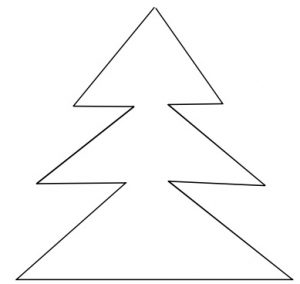
№6. Разрежьте ёлочку на рисунке тремя прямыми разрезами на 13 частей.

№7. Валя, Саша, Женя и Слава играли на перемене. Кто-то из них разбил окно. Валя: «Разбил кто-то из мальчиков». Саша: «Это Слава!» Женя: «Среди нас мальчиков больше». Слава: «Мы с Валей – девочки!». Оказалось, что все девочки солгали, а все мальчики сказали правду. Кто разбил окно? (все имена могут носить как мальчики, так и девочки) Ответ объясните.

№8. Нечетное количество конфет попытались разложить в коробки по 46 штук, удалось заполнить только 43 коробки. Потом их попытались уложить в коробки по 43 штуки. Хватило на 47 коробок и тоже что-то осталось. Получится ли разложить конфеты поровну в 17 коробок? Ответ объясните.

XXI ОЛИМПИАДА МЛАДШИХ ШКОЛЬНИКОВ
9 февраля 2014г. Старшая группа, 4 класс

№1. Нашего соседа пришли поздравить с днём рождения его отец, сын и внук. Их звали Антон Сергеевич, Андрей Борисович и Сергей Никитич. Как зовут нашего соседа, если у него только один сын и нет дочерей?

№2. Почтальон Печкин вышел из Простоквашино, а милиционер Свистулькин – из села Сметанино. Они встретились у километрового столба, с двух сторон которого были написаны расстояния до Сметанино и до Простоквашино. Печкин заметил, что это два разных числа, записанных одними и теми же цифрами, но в разном порядке. Каково наименьшее расстояние может быть между Простоквашино и Сметанино?

№3. Шарик склеил из кубиков параллелепипед со сторонами 2см, 4см и 6см. Матроскин склеил куб со стороной 3 см. Дядя Фёдор вырезал в картонке прямоугольную дырку, в которую пролезает творение Шарика, но не пролезает творение Матроскина. Какого размера дырку он мог вырезать? Достаточно привести 1 вариант

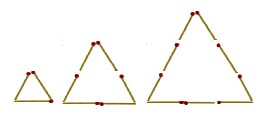
№4. На рисунке из спичек выложены один маленький треугольник, один средний и один большой. Выложите из этих спичек фигуру, в которой было бы ровно два маленьких треугольника, два средних и два больших. Лишних спичек быть не должно и каждая спичка должна участвовать хотя бы в одном треугольнике.

№5. На доске были написаны примеры на сложение. Вовочка заменил одинаковые цифры одинаковыми буквами, а разные – разными. Получилось, что
Д+В+А+Ж+Д+Ы+Д+В+А = 20 , а Т+Р+И+Ж+Д+Ы+Т+Р+И = 50 . Чему может быть равно Д+В+А+Ж+Д+Ы+Т+Р+И?

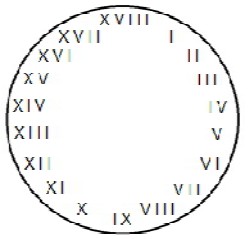
№6. При раскопках на территории Древнего Рима были найдены необычные часы, циферблат которых имел 18 делений и для нумерации использовались римские цифры (см.рис.). К сожалению, циферблат часов оказался расколот на 5 частей. Юный археолог Никита заметил, что суммы чисел на каждой из частей равны между собой. Покажите, как мог разбиться циферблат.

№7. Моряк Попай ест только шпинат, причём ровно раз в сутки – или завтракает, или обедает, или ужинает. Известно, что если в какой-то день Попай позавтракал, то на следующий день он будет только обедать. Если же он пообедал, то на следующий день он завтракать точно не будет. Если же он в какой-то день ужинает, то на следующий день он будет завтракать обязательно. Попай пообедал 1 января, и за все дни с 1 января по 8 февраля он позавтракал столько же, сколько и пообедал. В какое время суток Моряк Попай ел шпинат вчера (8 февраля)?

№8. Братья Авоська и Небоська в свой день рождения только лгут. В остальные дни говорят только чистую правду. Однажды Авоська сказал: «Сегодня 1 апреля. Завтра твой день рождения». Небоська ответил: «Сегодня твой день рождения. 1 апреля завтра». Когда родился Авоська?

XXI ОЛИМПИАДА МЛАДШИХ ШКОЛЬНИКОВ
24 февраля 2013г. Старшая группа, 4 класс

№1. В примере одинаковые цифры заменили одинаковыми буквами, а разные – разными. Получилось ОЛИМ + ПИ + АДА = 2013. Укажите, какие цифры могли стоять вместо букв

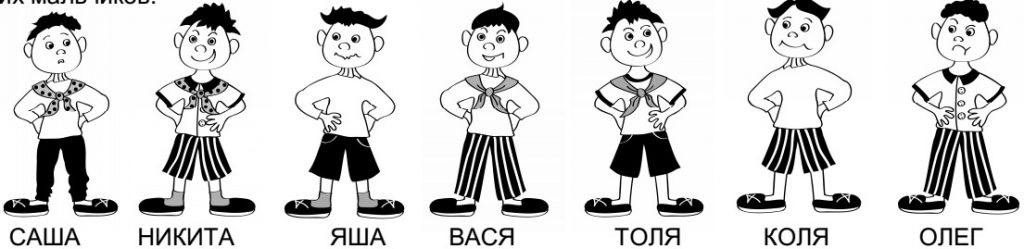
№2. У меня есть два друга, которые терпеть не могут одинаковую одежду и обувь. Поэтому они всегда одеваются так, что все у них отличается. Среди семерых ребят найдите этих мальчиков.

№3. У юного физика Илюши есть две одинаковые резинки. Он отметил у каждой из них середину и повесил на их концы гирьки так, чтобы одна резинка стала в три раза длиннее другой. Илюша измерил, насколько теперь одна отметка находится ниже другой. Во сколько раз это расстояние меньше длины более длинной резинки?

№4. Под Новый Год хакер Костя через равные промежутки времени провёл 17 вирусных атак на сайт Coca-Cola. Первая атака началась 31 декабря в 21:54, а последняя – 1 января в 11:30. Какой был промежуток времени между атаками?

№5. Аня, Боря, Вася, Галя и Даша решили съесть шоколадку. Но она упала на пол и, когда её развернули, оказалось, что она разбилась на семь кусков (см. рис.) Боря съел самый большой кусок. Галя и Даша съели одно и то же количество шоколада, но Галя съела три куска, а Даша – один. Вася съел седьмую часть всей шоколадки, а остальное съела Аня. Какой кусок шоколадки достался Ане?

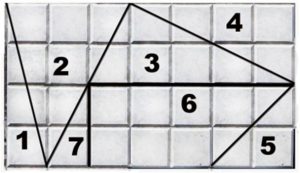
№6. На рисунке, выложенном из спичек можно насчитать шесть треугольников. Переложите четыре спички так, чтобы было видно ровно девять треугольников. Лишних спичек быть не должно.

№7. Жестянщик делает таблички с буквами. Одинаковые буквы он гравирует за одинаковое время, разные – возможно, за разное. На две таблички «ДОМ МОДЫ» и «ВХОД» он потратил 50 минут, а одну табличку «ДЫМОХОД В» сделал за 35 минут. За какое время он сделает табличку «ВЫХОД» ?

№8. Однажды на вечеринке разговаривали четверо друзей. Глория заявила: «Я всегда говорю меньше шести слов». Рико ответил: «А в моем предложении не больше восьми слов!» Алекс высказался: «Глория и Рико сейчас говорят правду». Марти мрачно добавил: «Но сегодня кто-то: Алекс или Глория солгал». Определите, кто в этот раз солгал, а кто сказал правду.

XXI ОЛИМПИАДА МЛАДШИХ ШКОЛЬНИКОВ
26 февраля 2012г. Старшая группа, 4 класс

№1. Поменяйте местами две цифры в равенстве 2012 = 1719 + 275, чтобы оно стало верным.

№2. У Пети на дне рождения был круглый торт, который резали прямолинейно через центр. На каждом куске было по свечке, а на одном куске ещё и розочка. Маша и Миша стали считать свечки по кругу (каждый начал со свечки), но оба забыли места, с которых начали. Маша насчитала 6 свечек и 2 розочки, а Миша – 19 свечек и 3 розочки. Сколько лет исполнилось Пете?

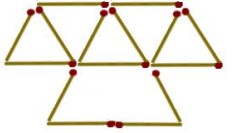
№3. Разрежьте клетчатую фигурку на рисунке справа на две одинаковые части, каждая из которых является разверткой кубика 1x1x1.

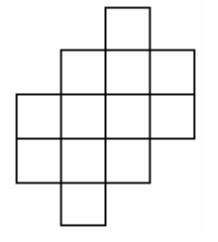
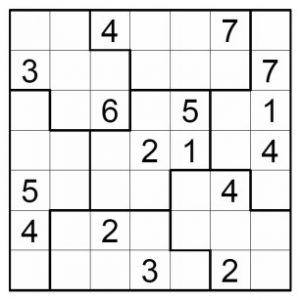
№4. В таблице слева расставьте числа от 1 до 7 так, чтобы в каждом столбце и каждой строчке, а также в каждой выделенной маленькой фигуре, были все семь чисел.

№5. У Никиты на линейке отмечены сантиметровые и миллиметровые деления. При этом Никита выяснил, что на линейке у него ровно 81 миллиметровое деление. Какое расстояние между первым и последним делением Никитиной линейки?

№6. У Винни-Пуха есть 11 больших горшков с мёдом и 10 маленьких. В магазине продаются коробки, в которые можно упаковать или 5 больших горшков, или 9 маленьких, или 4 больших и 3 маленьких. Сколько коробок придется купить Винни, чтобы упаковать все свои горшки? (Он хочет купить как можно меньше коробок).

№7. На олимпиаду пришли Андрей, Боря и Витя. Один из них первоклассник, другой – второклассник, а третий – третьеклассник. Известно, что второклассник решил на одну задачу меньше, чем Андрей, а Витя решил на две задачи больше, чем третьеклассник. Кто решил больше задач и на сколько: Боря или первоклассник?

№8. У Саши есть 2 золотых, 3 серебряных и 4 бронзовых монеты. Одна из них фальшивая, причем, если фальшивая монета серебряная, то она легче настоящей серебряной, а если фальшивая золотая или бронзовая, то она тяжелее соответственно настоящей золотой или бронзовой. За два взвешивания на чашечных весах без гирь найдите фальшивую монету. Примечание. Монеты из разного металла могут весить по-разному, однако настоящие монеты из одного металла весят одинаково.