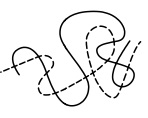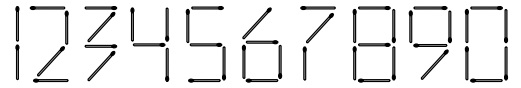Задачи международного конкурса «Кенгуру»
15 марта 2018 г. 3–4 классы. Время, отведенное на решение задач — 75 минут!
Задачи, оцениваемые в 3 балла
№1. Сколько различных цифр в записи даты конкурса «Кенгуру»?
15 03 2018
(А) 5 (Б) 6 (В) 7 (Г) 8 (Д) 10
№2. Сколько раз пересекаются сплошная и пунктирная линии?
А) 6 (Б) 7 (В) 8 (Г) 9 (Д) 10
№3. В Петербурге 15 марта в 16 часов пошел снег, а 16 марта в 15 часов снегопад прекратился. Сколько часов он продолжался?
А) 11 (Б) 12 (В) 23 (Г) 249 (Д) 25
№4. На одном из рисунков А-Д божья коровка отличается от других четырех. На каком?
 №5. На рисунке изображен план парка с семью аллеями. Маша вышла из точки О и прошла по двум аллеям. В какой точке она не могла оказаться?
№5. На рисунке изображен план парка с семью аллеями. Маша вышла из точки О и прошла по двум аллеям. В какой точке она не могла оказаться?
А) А (Б) Б (В) В (Г) Г (Д) Д
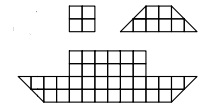 №6. Тимур вырезал из клетчатой бумаги несколько четырехугольников двух видов (см. рисунок). Сколько четырехугольников ему надо взять, чтобы сложить корабль?
№6. Тимур вырезал из клетчатой бумаги несколько четырехугольников двух видов (см. рисунок). Сколько четырехугольников ему надо взять, чтобы сложить корабль?
А) 5 (Б) 6 (В) 7 (Г) 8 (Д) 9
№7. Чему равна сумма наибольшей и наименьшей из трех цифр, которых нет в записи числа 2018?
А) 7 (Б) 9 (В) 10 (Г) 12 (Д) 15
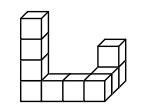 №8. Миша склеил конструкцию из 10 белых кубиков. Потом он покрасил ее со всех сторон. Сколько кубиков имеют ровно 4 окрашенные грани?
№8. Миша склеил конструкцию из 10 белых кубиков. Потом он покрасил ее со всех сторон. Сколько кубиков имеют ровно 4 окрашенные грани?
(A) 6 (Б) 7 (В) 8 (Г) 9 (Д) 10
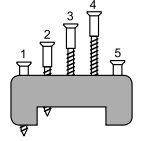 №9. Четыре шурупа на рисунке имеют одинаковую длину, а один короче остальных. Какой?
№9. Четыре шурупа на рисунке имеют одинаковую длину, а один короче остальных. Какой?
(A) 1 (Б) 2 (В) 3 (Г) 4 (Д) 5
№10. В примере на вычитание двузначных чисел Оля закрасила две цифры. Чему равно произведение закрашенных цифр?
(А) 6 (Б) 7 (В) 8 (Г) 9 (Д) 10
Задачи, оцениваемые в 4 балла
№11. Даня стрелял из лука по мишени. В первый раз он набрал 12 очков, во второй — 15 очков. 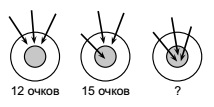 Сколько очков он набрал в третий раз?
Сколько очков он набрал в третий раз?
(A) 18 (Б) 19 (В) 20 (Г) 21 (Д) 27
№12. Если середина первой половины июня — среда, то середина второй половины июня того же года — это
(А) понедельник (Б) вторник (В) четверг (Г) пятница (Д) суббота
№13. У Алика есть много наклеек пяти разных видов. Он вклеивает их по одной в каждую клетку квадрата так, чтобы  фигурки в каждом столбце и в каждой строчке не повторялись. Какая наклейка
фигурки в каждом столбце и в каждой строчке не повторялись. Какая наклейка
должна оказаться в закрашенной клетке?
№14. У Ани есть два младших брата-близнеца. Они родились в тот день, когда Ане исполнилось 8 лет. Сколько лет ей исполнится, когда ее возраст станет равен сумме возрастов близнецов?
(A) 12 (Б) 14 (В) 16 (Г) 18 (Д) 20
№15. Прямоугольник состоит из пяти квадратов. Три маленьких квадрата имеют сторону, равную 1 см. 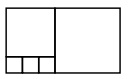 Чему равен периметр прямоугольника?
Чему равен периметр прямоугольника?
(A)11 см (Б)22 см (В)24 см (Г)28 см (Д)32 см
№16. Чему равна сумма двух чисел, если она на шесть больше одного из них и в три раза больше другого?
(А) 9 (Б) 12 (В) 16 (Г) 18 (Д) 24
№17. В каждой клетке доски записано число (см. рисунок). Жук Жак заполз на клетку доски с числом 1. 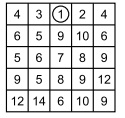 Потом он добрался до нижнего ряда, переползая каждый раз через сторону клетки так, чтобы число в новой клетке было больше числа в предыдущей. В клетке с каким числом он оказался?
Потом он добрался до нижнего ряда, переползая каждый раз через сторону клетки так, чтобы число в новой клетке было больше числа в предыдущей. В клетке с каким числом он оказался?
(А) 12 (Б) 14 (В) 6 (Г) 10 (Д) 9
№18. Федя время от времени смотрит на часы, висящие на стене, и записывает, куда указывает секундная стрелка. У него получился такой список: вверх, влево, вниз, вверх, вверх. Какое наименьшее время могло пройти между первой и последней записями?
(А) 2 мин (Б) 2 мин 15 сек (В) 2 мин 45 сек (Г) 3 мин (Д) 4 мин
№19. Четыре гирьки, которые весят 10 г, 20 г, 30 г и 40 г, взвешивали на чашечных весах (см. рисунок). 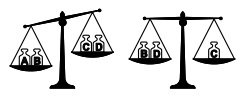
Сколько весит гирька С?
(A) 10 г (Б) 20 г (В) 30 г (Г) 40 г (Д) невозможно определить
№20. Вася, Коля, Митя и Петя взяли синий, красный, желтый и зеленый мячи , каждый по одному. У меня мяч не красный, — сказал Вася. — У меня мяч не синий, — сказал Петя. — У меня мяч не зеленый, — сказал Коля. — У меня мяч не желтый и не синий, — сказал Митя. Соврал только тот, у кого красный мяч. Какой мяч у Коли?
(А) синий (Б) красный (В) зеленый (Г) желтый (Д) невозможно определить
Задачи, оцениваемые в 5 баллов
№21. В числах 345 и 921 выбрали по одной цифре и поменяли их местами друг с другом. При этом сумма чисел увеличилась. Чему стала равна эта сумма?
(А) 1267 (Б) 1293 (В) 1295 (Г) 1300 (Д) 1464
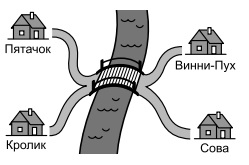 №22. Путь от дома Пятачка до дома Винни-Пуха равен 160 м, от дома Винни-Пуха до дома Совы 200 м, а от дома Совы до дома Кролика 190 м. Мост через реку имеет длину 10 м. Сколько метров от домика Пятачка до домика Кролика?
№22. Путь от дома Пятачка до дома Винни-Пуха равен 160 м, от дома Винни-Пуха до дома Совы 200 м, а от дома Совы до дома Кролика 190 м. Мост через реку имеет длину 10 м. Сколько метров от домика Пятачка до домика Кролика?
(A) 130 (Б) 140 (В) 160 (Г) 170 (Д) 180
№23. Дима придумал способ выкладывать цифры спичками: Потом, используя 17 спичек, он выложил самое большое возможное число. Какова будет первая цифра этого числа?
(A) 1 (Б) 2 (В) 7 (Г) 8 (Д) 9
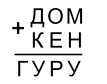 №24. В ребусе одинаковые цифры зашифрованы одинаковыми буквами, а разные — разными. Известно, что ДОМ = 256. Одна цифра в ребусе не использована. Какая?
№24. В ребусе одинаковые цифры зашифрованы одинаковыми буквами, а разные — разными. Известно, что ДОМ = 256. Одна цифра в ребусе не использована. Какая?
(A) 0 (Б) 3 (В) 4 (Г) 7 (Д) 9
№25. Сколько всего квадратов, образованных жирными линиями, изображено на рисунке?
(A) 16 (Б) 20 (В) 23 (Г) 24 (Д) 25