ЗАДАЧИ МЕЖДУНАРОДНОГО КОНКУРСА «Кенгуру»
21 марта 2019 г. 3–4 классы. Время, отведенное на решение задач, — 75 минут!
№1. В зоопарке 21 ноября 2018 года родился кенгуренок. Сколько месяцев ему исполнилось 21 марта 2019 года?
(А) 3 (Б) 4 (В) 5
(Г) 6 (Д) 7
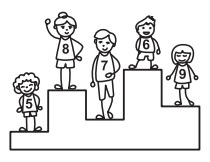
№2. Для награждения победителей соревнования сделали пьедестал: чем лучше результат участника, тем выше ступенька, на которой он стоит. Участник с каким номером занял третье место?
(А) 5 (Б) 6 (В) 7 (Г) 8 (Д) 9
№3. Индейцы майя записывали числа с помощью точек и отрезков. Число пять изображалось отрезком, а единица – точкой. Например, рисунок ••• изображал число 8. Какое число изображалось рисунком, приведенным ниже ?
(А) 7 (Б) 12 (В) 15 (Г) 19 (Д) 22
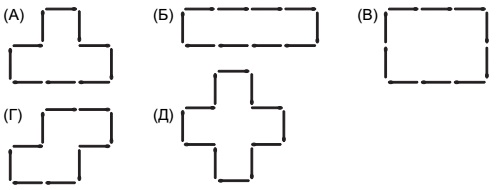
№4. Какой из кусочков А-Д можно вырезать из квадрата, изображенного справа?
№5. Если вчера была суббота, то какой день недели будет послезавтра?
(А) вторник (Б) среда (В) пятница)
(Г) суббота (Д) воскресенье
№6. Через какую точку придется пройти Винни-Пуху, чтобы, двигаясь по стрелочкам, попасть в гости к Пят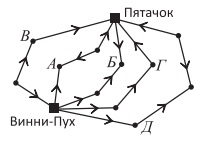
ачку?
(А) А (Б) Б (В) В
(Г) Г (Д) Д
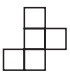№7. Сколько из нарисованных ниже фигур можно получить, если отрезать одну клетку от фигуры, изображенной слева?
(А) одну (Б) две (В) три (Г) четыре (Д) пять
№8. Какое из следующих чисел самое маленькое?
(А) 500005 (Б) 50050 (В) 500050 (Г) 50005 (Д) 55000
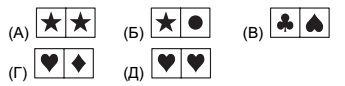
№9. Какую из фигур А-Д нельзя сложить из 10 спичек?
№10. Из цифр 2, 0, 1, 9, используя каждую только один раз, можно составить некоторые даты (число и месяц), например, 09.12. Маша обнаружила, что из этих цифр можно составить день ее рождения. Она родилась в октябре. Какого числа она родилась?
(А) 10 (Б) 12 (В) 19 (Г) 20 (Д) 29
Задачи, оцениваемые в 4 балла
№11. Женя выписала все трехзначные числа, у каждого из которых первая цифра равна 4, все цифры различны и расположены в порядке убывания. Сколько чисел выписала Женя?
(А) 1 (Б) 3 (В) 4 (Г) 6 (Д) 16
№12. На рисунке изображена открытая книжка. В ее обложке два окошка. Какие три фигуры будут видны, если книжку закрыть?
№13. В аквариуме 15 рыбок: барбусы, меченосцы и сомики. Известно, что 10 из них – не сомики, а 9 – не барбусы. Сколько меченосцев в аквариуме?
(А) 1 (Б) 2 (В) 3 (Г) 4 (Д) 5
№14. У Миши есть 6 доминошек, которые изображены на рисунке справа. Он выложил их в линию, следуя обычным правилам игры в домино (число точек в соседних квадратиках двух разных доминошек всегда одинаково). В первом квадратике слева стоит одна точка. Сколько точек в самом правом квадратике?
(А) 1 (Б) 2 (В) 3 (Г) 4 (Д) 5
№15. В классе 5 человек изучают китайский язык и 6 человек – японский. Всего в классе изучают эти языки 8 человек. Сколько человек изучают оба этих языка?
(А) 5 (Б) 4 (В) 3 (Г) 2 (Д) 1
№16. На рисунке одинаковые значки обозначают одинаковые числа, а разные значки – разные числа.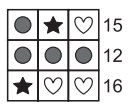 
Сумма чисел, стоящих в строчке, написана справа от нее. Какое число обозначено звездочкой ?
(А) 2 (Б) 3 (В) 4 (Г) 5 (Д) 6
№17. У одного из пяти мальчиков есть футбольный мяч.
Алеша сказал: «У меня нет мяча».
Боря сказал: «Мяч у меня».
Витя сказал: «Мяч не у Дани».
Гоша сказал: «У меня нет мяча».
Даня сказал: «Мяч у Алеши».
Только один мальчик сказал неправду. Кто?
(А) Алеша (Б) Боря (В) Витя (Г) Гоша (Д) Даня
№18. В числе 2019 две цифры поменяли местами, а потом одну цифру стерли. Какое самое большое число могло получиться?
(А) 901 (Б) 910 (В) 912 (Г) 920 (Д) 921
№19. Все три гномика на рисунке весят одинаково. Вес гномика – целое число килограммов. Сколько весит гномик?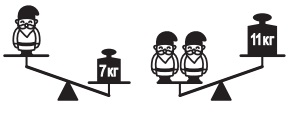
(А) 3 кг (Б) 4 кг (В) 5 кг (Г) 6 кг (Д) 8 кг
№20. Все страницы пронумерованы. Цифра 5 встречается в номерах страниц ровно 13 раз. Сколько страниц в этой книге?
(А) 50 (Б) 56 (В) 57 (Г) 58 (Д) 60
Задачи, оцениваемые в 5 баллов
№21. Шнурок продет через дырки в дощечке, как показано на рисунке справа.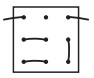 
Как может выглядеть эта дощечка с обратной стороны?
№22. Назовем двузначное число супердвузначным, если и при умножении его на 2, и при делении его на 2 снова получается двузначное число. Сколько всего супердвузначных чисел?
(А) 15 (Б) 16 (В) 18 (Г) 20 (Д) 25
№23. На рисунке изображен коридор и указаны некоторые размеры. Кот прошел вдоль пунктирной линии, точно по середине коридора. Сколько метров прошел кот?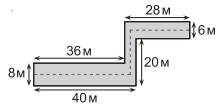
(А) 63 м (Б) 68 м (В) 69 м
(Г) 71 м (Д) 83 м
№24. В вершине куба на рисунке Женя вписала числа от 1 до 8, каждое по одному разу. Для каждой из шести граней она нашла сумму четырех чисел, написанных в вершинах этой грани. Три из этих сумм – это 16, 18 и 22. Чему равна самая маленькая из всех шести сумм?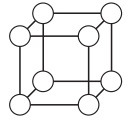
(А) 10 (Б) 12 (В) 14 (Г) 15 (Д) 16
№25. Малыш, Карлсон и фрекен Бок едят плюшки. Малыш съедает 2 плюшки за то же время, за которое фрекен Бок съедает 7. Пока она ест 3 плюшки, Карлсон съедает 5. За некоторое время Малыш и фрекен Бок съели 27 плюшек. Сколько плюшек за это время съел Карлсон?
(А) 10 (Б) 15 (В) 35 (Г) 40 (Д) 45
№26. В клетки квадрата на рисунке Вася хочет вписать числа от 1 до 5 так, чтобы в каждой строке и каждом столбце все числа были различны. Квадрат разбит на три области. Суммы чисел в областях должны быть равны. В левую нижнюю клетку Вася вписал число 2. Какое число он впишет в правую верхнюю клетку?
(А) 1 (Б) 2 (В) 3 (Г) 4 (Д) 5
