Олимпиада МИРЭА (Творческая лаборатория 2х2) 2016 год, 3 класс
№1. Найдите хотя бы одно решение ребуса
АААА + БББ + АА + В = 2016.
(Одинаковым буквам соответствуют одинаковые цифры, разным – разные)
№2. У Деда Мороза было 5 шоколадок в стопке в обёртках разных цветов: красной (К), жёлтой (Ж), синей (С), оранжевой (О) и зелёной (З). Пятеро детей встали в круг, и Дед Мороз стал раздавать шоколадки через одного. В каком порядке могли лежать шоколадки, если последняя была в жёлтой обёртке, а в результате все получили шоколадки как на рисунке?
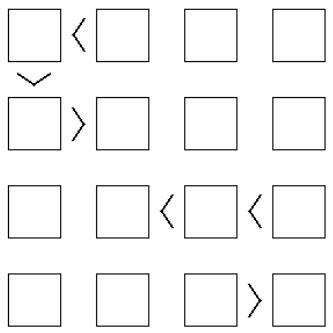 №3. Расставьте в клеточки цифры 1, 2, 3, 4 так, чтобы в каждой строке и в каждом столбце присутствовали все 4 цифры и были выполнены указанные неравенства.
№3. Расставьте в клеточки цифры 1, 2, 3, 4 так, чтобы в каждой строке и в каждом столбце присутствовали все 4 цифры и были выполнены указанные неравенства.
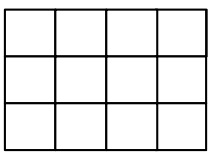 №4. Разрежьте прямоугольник размером 3 × 4 клетки по линиям сетки на две фигуры равного периметра, но неравной площади.
№4. Разрежьте прямоугольник размером 3 × 4 клетки по линиям сетки на две фигуры равного периметра, но неравной площади.
№5. Обычно Малыш перед сном смотрит по телевизору 5 мультиков. Но если Малыш шалит днём, Фрекен Бок запрещает ему смотреть некоторые мультики. За показывание языка Фрекен Бок Малыш лишается мультиков №1, 2 и 3. За таскание плюшек – мультиков №2, 4 и 5. За гуляние по крыше – мультиков №1 и 5. За взрыв паровой машины – мультиков №1 и 4. За игру с котом – мультика №5. Утром Малыш решил, что хочет сегодня посмотреть хотя бы один мультик. Какое наибольшее количество шалостей из перечисленных может позволить себе Малыш в этот день?
№6. Эдуард всегда говорит по два утверждения, одно из которых верно, а другое нет. Однажды он сказал: «Вчера была среда. Послезавтра будет вторник». Потом он подумал немного и сказал: «Сегодня среда. Вторник был позавчера». В какой день недели это было?
 №7. В правой нижней клетке доски сидит жук (как на рисунке). Он прополз вдоль линий сетки через ещё четыре разные клетки, а на пятой решил отдохнуть. Укажите, какая это может быть клетка, если известно, что за всё время путешествия жук совершил поровну как левых, так и правых поворотов.
№7. В правой нижней клетке доски сидит жук (как на рисунке). Он прополз вдоль линий сетки через ещё четыре разные клетки, а на пятой решил отдохнуть. Укажите, какая это может быть клетка, если известно, что за всё время путешествия жук совершил поровну как левых, так и правых поворотов.
№8. На столе в ряд лежат 4 монеты, из них 2 фальшивые, которые весят одинаково и легче настоящих. При этом известно, что фальшивые монеты не лежат рядом. Как за одно взвешивание на чашечных весах без гирь найти обе фальшивые монеты?


