Олимпиада МИРЭА (Творческая лаборатория 2х2) 2017 год, 3 класс

№1. Добавьте знаки действий, чтобы получилось верное равенство: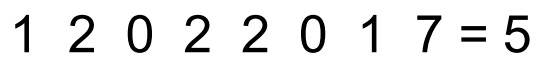 (можно использовать знаки действий и скобки любое количество раз)

№2. Справа нарисован крестик из пяти клеток, а в вашем бланке ответов нарисована доска 7 на 7 клеток. Закрасьте несколько клеток на этой доске так, чтобы после этого в каком бы месте доски мы ни выбрали бы такой же крестик, он обязательно накроет ровно одну закрашенную вами клетку.

№3. Тихон выкладывает из спичек цифры:

Он выложил число сто:

Переложите 4 спички так, чтобы получилось как можно большее число.

№4. Встретились как-то коты: Хассельблад, Васька и Финик. У одного из них были голубые глаза, у второго желтые, а у третьего один глаз был желтым, а второй зеленым. Если бы у Финика были такие же глаза, как у Хассельблада, то общее количество глаз каждого присутствующего цвета было бы одинаково. Какого цвета глаза у каждого кота?

№5. В каком порядке падали сверху вниз фигурки пентамино в игре, если в результате они расположились так, как показано на рисунке?

№6. Места в единственном вагоне Паровозика из Ромашкова решили пронумеровать, для чего изготовили карточки с цифрами. Оказалось, что карточек с цифрой 1 потребовалось на 11 штук больше, чем карточек с цифрой 0. Какое наименьшее количество мест может быть в этом вагоне?

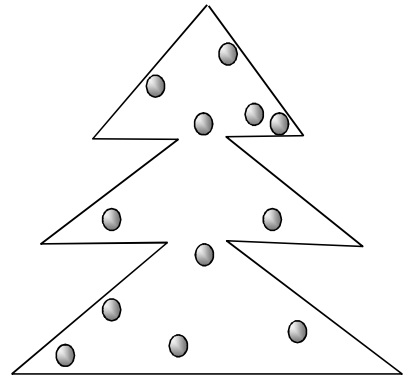
№7. Разрежьте ёлочку на рисунке двумя прямыми разрезами на несколько частей так, чтобы во всех частях было одинаковое количество шариков.

 

 

№8. Петя считает количество квартир в своем подъезде: 1,2,3, … Если номер квартиры делится на 11, Петя чихает, а если номер этажа делится на 4, Петя кашляет. Этаж, на котором Петя впервые одновременно чихнул и закашлял был предпоследним. Сколько этажей в подъезде Пети, если на каждом этаже в его подъезде (включая первый этаж) по 4 квартиры?