Задачи международного конкурса «Кенгуру»

15 марта 2012 г. 3–4 классы.  Время, отведенное на решение задач — 75 минут!

Задачи, оцениваемые в 3 балла

№1. Саша рисует на плакате слова УРА КЕНГУРУ. Одинаковые буквы он рисует одним цветом, а разные буквы — разными цветами. Сколько различных цветов ему понадобится?

(A) 6      (Б) 7       (В) 8       (Г) 9       (Д) 10

№2. Один будильник спешит на 25 минут и показывает 7 часов 50 минут. Какое время показывает другой будильник, который отстает на 15 минут?

(A) 7 час 10 мин                (Б) 7 час 25 мин                (В) 7 час 35 мин

(Г) 7 час 40 мин                 (Д) 8 час

№3. Только на одной из этих пяти картинок площадь закрашенной части не равна площади белой части. На какой?

№4. Три воздушных шарика стоят на 12 рублей больше, чем один шарик. Сколько стоит один шарик?

(A) 4 руб.             (Б) 6 руб.              (В) 8 руб.             (Г) 10 руб.            (Д) 12 руб.

№5. На каком из рисунков клеточки A2, B1 и C3 закрашены?

№6. В школе для зверей учатся 3 котенка, 4 утенка, 2 гусенка и несколько щенков. Когда учитель пересчитал лапы всех своих учеников, получилось 44. Сколько щенков учится в школе?

(A) 6      (Б) 5       (В) 4       (Г) 3       (Д) 2

№7. Что не равно семи?

(A) число дней в неделе (Б) число букв в слове КЕНГУРУ (В) полдюжины

(Г) номер этой задачи (Д) число цветов радуги

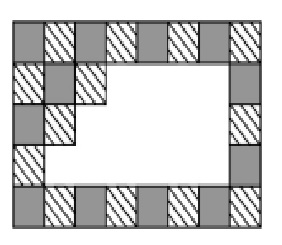
№8. Плитки двух видов были выложены на стене в шахматном порядке. Несколько плиток упали со стены (см. рисунок). Сколько полосатых плиток упало?

(A) 9      (Б) 8       (В) 7       (Г) 6       (Д) 5

 

№9. Петя задумал число, прибавил к нему 3, сумму умножил на 50, снова прибавил 3, умножил результат на 4 и получил 2012. Какое число задумал Петя?

(A) 11    (Б) 9       (В) 8       (Г) 7       (Д) 5

№10. В феврале 2012 года в зоопарке родился маленький кенгуру. Сегодня, 15 марта, ему исполняется 20 дней. В какой день он родился?

(A) 19 февраля   (Б) 21 февраля    (В) 23 февраля   (Г) 24 февраля    (Д) 26 февраля

Задачи, оцениваемые в 4 балла

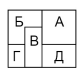
№11. На лист бумаги Вася наклеил один за другим 5 одинаковых квадратов. Видимые части этих квадратов на рисунке помечены буквами. В каком порядке Вася наклеивал квадраты?

(A) А, Б, В, Г, Д                (Б) Б, Г, В, Д, А                 (В) А, Д, В, Б, Г

(Г) Г, Д, Б, В, А                 (Д) Г, Б, В, Д, А

№12. Блоха прыгает по длинной лестнице. Она может прыгать или на 3 ступеньки вверх, или на 4 ступеньки вниз. За какое наименьшее число прыжков она может перебраться с земли на 22-ю ступеньку?

(A) 7      (Б) 9       (В) 10    (Г) 12    (Д) 15

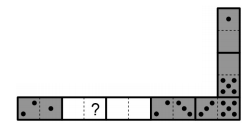№13. Федя выложил правильную цепочку из семи доминошек (число точек в соседних квадратиках двух разных доминошек всегда одинаково). На всех доминошках вместе было 33 точки. Потом Федя забрал две доминошки из полученной цепочки (см. рисунок). Сколько точек было в квадратике, в котором стоит знак вопроса?

(A) 2     (Б) 3       (В) 4       (Г) 5       (Д) 6

№14. За год до рождения Кати ее родителям вместе было 40 лет. Сколько сейчас лет Кате, если через 2 года ей и ее родителям вместе будет 90 лет?

(A) 15    (Б) 14    (В) 13    (Г) 8       (Д) 7

№15. Четвероклассница Маша и ее брат первоклассник Миша решали задачи конкурса «Кенгуру» для 3–4 классов. В результате оказалось, что Миша получил не 0 баллов, а Маша — не 100 баллов. На какое наибольшее число баллов Маша могла обогнать Мишу?

(A) 92    (Б) 94    (В) 95    (Г) 96    (Д) 97

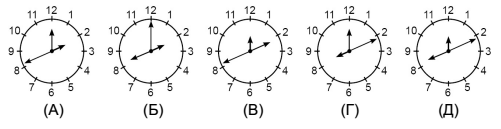
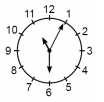№16. У правильно идущих «странных» часов перепутаны стрелки (часовая, минутная и секундная). В 12 : 55 : 30 стрелки располагались так, как показано на рисунке справа. Что покажут эти часы в 20 часов 12 минут?

№17. На рыбалку отправились пятеро мужчин из одной семьи: дедушка, 2 его сына и 2 внука. Их зовут: Борис Григорьевич, Григорий Викторович, Андрей Дмитриевич, Виктор Борисович, и Дмитрий Григорьевич. Как в детстве звали дедушку?

№18. Параллелепипед состоит из четырех частей. Каждая часть состоит из 4 кубиков одинакового цвета (см. рисунок). Какую форму имеет белая часть?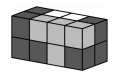

 №19. В футболе команда получает за победу 3 очка, за ничью — 1 очко, а за поражение — 0 очков. Команда сыграла 38 матчей и получила 80 очков. Какое наибольшее число раз эта команда могла проиграть?

(A) 12    (Б) 11    (В) 10    (Г) 9       (Д) 8

№20. К пятизначному числу, сумма цифр которого равна 2, прибавили двузначное число. Получилось снова пятизначное число, сумма цифр которого равна 2. Какое число получилось?

(A) 20000             (Б) 11000              (В) 10100             (Г) 10010              (Д) 10001

Задачи, оцениваемые в 5 баллов

№21. Недалеко от Венеции расположены три острова: Мурано, Бурано и Торчелло. Посетить Торчелло можно только побывав по дороге и на Мурано, и на Бурано. Каждый из 15 туристов посетил хотя бы один остров. При этом 5 человек посетили Торчелло, 13 человек побывали на Мурано и 9 человек — на Бурано. Сколько туристов посетили ровно два острова?

(A) 2      (Б) 3       (В) 4       (Г) 5       (Д) 9

№22. Бумажный кубик разрезали и развернули. Какие из фигур 1–5 могли получиться?

(A) все                 (Б) только 1, 2, 4                (В) только 1, 2, 4, 5           (Г) только 1, 4, 5               (Д) только 1, 2, 3

№23. Никита выбрал два трехзначных числа, у которых совпадают суммы цифр. От большего числа он отнял меньшее. Какое самое большое число мог получить Никита?

(A) 792     (Б) 801     (В) 810      (Г) 890       (Д) 900

№24. В полдень из столицы в город А вышли скороход и торговец. Одновременно по той же дороге навстречу им из А вышел отряд стражников. Через час стражники встретили скорохода, еще через 2 часа они встретили торговца, а еще через 3 часа стражники прибыли в столицу. Во сколько раз быстрее торговца идет скороход?

(A) 2      (Б) 3       (В) 4       (Г) 5       (Д) 6

25. Сколько всего квадратиков, образованных выделенными линиями, изображено на рисунке?

(A) 43   (Б) 58    (В) 62    (Г) 63    (Д) 66

№26. В равенстве КЕН = ГУ × РУ разными буквами обозначены разные ненулевые цифры, а одинаковыми буквами — одинаковые цифры. Найдите Е, если известно, что число КЕН — самое маленькое из
возможных.

(A) 2    (Б) 5    (В) 6    (Г) 8    (Д) 9