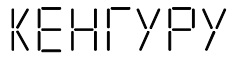ЗАДАЧИ МЕЖДУНАРОДНОГО КОНКУРСА «Кенгуру»
20 марта 2014 г. 3–4 классы. Время, отведенное на решение задач, — 75 минут!
Задачи, оцениваемые в 3 балла
№1. Боря выложил из одинаковых палочек слово КЕНГУРУ. Сколько букв сложены из 5 палочек?
(A) 2 (Б) 3 (В) 4 (Г) 5 (Д) 6
№2. Как в математике называется число, которое вычитают?
(A) вычтенное (Б) вычитуемое (В) вычитываемое (Г) вычитающееся (Д) вычитаемое
№3. Как выглядит центральная часть звезды, изображенной на рисунке справа?
№4. Во сколько раз 10 метров больше 1 мм?
(A) 100000 (Б) 10000 (В) 1000 (Г) 100 (Д) 10
№5. Аня хочет вставить цифру 3 в число 2014 так, чтобы получившееся пятизначное число было как можно меньше. Где она должна написать цифру 3?
(А) перед цифрой 2 (Б) между цифрами 2 и 0 (В) между цифрами 0 и 1 (Г) между цифрами 1 и 4 (Д) после цифры 4
№6. Андрей написал правильный пример, а его младший брат заклеил бумажными кружочками все знаки действий. Получилось: 1m6m1m2m4 = 6. В каком порядке могли стоять знаки в этом примере?
(А) + + — + (Б) + — — + (В) + + + — (Г) + — + — (Д) + — — —
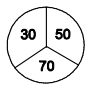
№7. Паша бросает дротики в мишень, изображенную справа. Сколько очков он не мог набрать за два броска?
(A) 60 (Б) 80 (В) 90 (Г) 100 (Д) 120
№8. Никита выписал числа от 1 до 31. На сколько больше он написал единиц, чем троек?
(A) 8 (Б) 9 (В) 10 (Г) 11 (Д) 13
№9. Прямоугольник согнули пополам по жирной линии. Какая цифра оказалось не закрытой закрашенным квадратиком?
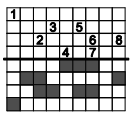
(A) 1 (Б) 3 (В) 6 (Г) 7 (Д) 8
№10. Адам собрал меньше орехов, чем Мартин, но больше, чем Сьюзен. Дана собрала больше, чем Мартин, и меньше, чем Люси. Кто из них собрал больше всего орехов?
(A) Люси (Б) Мартин (В) Сьюзен (Г) Дана (Д) Адам
Задачи, оцениваемые в 4 балла
№11. На планете Кенгуру один год состоит из 20 месяцев, а каждый месяц — из 6 недель. Четверть года у кенгурят каникулы. Сколько недель продолжаются каникулы?
(A) 5 (Б) 6 (В) 10 (Г) 24 (Д) 30
№12. Семеро детей сидят за круглым столом. Никакие два мальчика не сидят рядом, и никакие три девочки не сидят подряд. Сколько девочек за столом?
(A) 2 (Б) 3 (В) 4 (Г) 5 (Д) 6
№13. Алиса заметила, что два месяца подряд 20-е число приходилось на четверг. Какой день недели будет 20-го числа в следующем за ними месяце?
(A) понедельник (Б) вторник (В) среда (Г) пятница (Д) воскресенье
№14. На рисунке справа AC=12, BD=15, CE=11и AB=DE. Чему равна длина CD?
(A) 7 (Б) 8 (В) 10 (Г) 11 (Д) 23
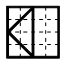№15. Квадрат разрезан на четыре части, как показано на рисунке. Какую фигуру нельзя составить из этих частей?
№16. Вася взял в школу 18 конфет. Три конфеты он съел по дороге. Каждый раз, когда Вася съедал конфету в школе, он угощал конфетой Машу или Дашу, причем три раза он угостил сразу обеих девочек. Все конфеты были съедены. Сколько конфет съел Вася?
(A) 7 (Б) 8 (В) 9 (Г) 10 (Д) 11
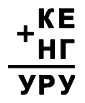
№17. В ребусе одинаковые буквы обозначают одинаковые цифры, а разные буквы — разные цифры. Известно, что цифры 0, 8 и 9 не использованы. Какая еще цифра не использована?
(A) 2 (Б) 3 (В) 4 (Г) 5 (Д) 6
№18. Летом дети ездили на велосипедах с дачи на озеро. От дачи до озера 3 км. Игорь проезжал весь путь за 10 минут, Маша ехала в 2 раза дольше, а Аня ехала быстрее Маши, но медленнее Игоря. Какая скорость могла быть у Ани?
(A) 20 км/ч (Б) 18 км/ч (В) 12 км/ч (Г) 9 км/ч (Д) 6 км/
№19. После того, как в 7:00 прозвенел будильник, Вася стукнул по нему кулаком, и минутная стрелка стала двигаться в 12 раз быстрее, чем надо. Что покажет этот будильник в 7:55?
№20. У малыша Феди есть 10 красных кубиков, 15 синих и 30 зеленых. Он хочет построить из них башню так, чтобы любые два соседних кубика имели разный цвет. Сколько кубиков будет в самой высокой башне, которую сможет построить Федя?
(A) 30 (Б) 32 (В) 50 (Г) 51 (Д) 55
Задачи, оцениваемые в 5 баллов
№21. Братец Кролик за день съедает или 9 морковок, или 2 кочана капусты, или 1 кочан капусты и 4 морковки. За неделю он съел 30 морковок. Сколько кочанов капусты он съел за эту неделю?
(A) 6 (Б) 7 (В) 8 (Г) 9 (Д) 10
№22. Какое наименьшее число клеток надо закрасить, чтобы в любом квадратике 2 ´ 2 на рисунке была хотя бы одна закрашенная клетка?
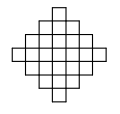
(A) 8 (Б) 6 (В) 5 (Г) 4 (Д) 3
№23. Фрекен Бок поставила на стол 15 тарелок с булочками. На первой тарелке лежит одна булочка, на второй — две, на третьей — три, и так далее. Иногда в окно влетает Карлсон, выбирает несколько тарелок и съедает с каждой из них одинаковое количество булочек. За какое наименьшее число визитов Карлсон сможет съесть все булочки?
(A) 3 (Б) 4 (В) 5 (Г) 10 (Д) 15
№24. Какой кубик получится из данной развертки?
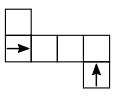
№25. Назовем трехзначное число удивительным, если оно делится на 3, а первая и последняя цифры у него одинаковы. Чему равна наименьшая разность между двумя удивительными числами?
(A) 12 (Б) 15 (В) 21 (Г) 30 (Д) 51
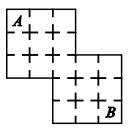
№26. На рисунке изображен план дома Кенги. Любые две соседние комнаты соединены дверью. Кенга хочет пройти из комнаты А в комнату В, не проходя ни через какую комнату более одного раза. Сколькими способами Кенга сможет это сделать?
(A) 24 (Б) 36 (В) 81 (Г) 144 (Д) 288
