ЗАДАЧИ МЕЖДУНАРОДНОГО КОНКУРСА «Кенгуру»
19 марта 2015 г. 3–4 классы
Задачи, оцениваемые в 3 балла
№1. Незнайка писал слово КЕНГУРУ. У него получилось: Сколько букв он написал неправильно?
![]()
(A) 1 (Б) 2 (В) 3 (Г) 4 (Д) 5
№2. Чему равна сумма двадцати сотен и пятнадцати?
(A) 35 (Б) 215 (В) 2015 (Г) 20015 (Д) 200015
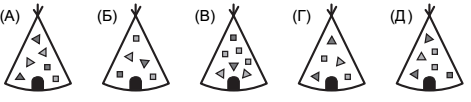
№3. Индеец Белый Орёл живет в вигваме, на котором треугольников и квадратиков нарисовано поровну. На каком из рисунков изображён его вигвам?
№4. Что не равно 12?
(А) дюжина
(Б) число месяцев в году
(В) число часов в сутках
(Г) утроенный номер этой задачи
(Д) число подвигов Геракла
№5. На рисунке изображён пруд и несколько лягушек. Сколько из этих лягушек сидят в пруду?
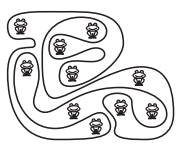
(A) 5 (Б) 6 (В) 7 (Г) 8 (Д) 9
№6. В числе 2015 четыре цифры. Произведение двух бóльших цифр поделили на сумму двух меньших. Что получилось?
(A) 6 (Б) 7 (В) 8 (Г) 10 (Д) 15
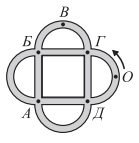
№7. Петя катается на велосипеде по дорожкам, изображённым на рисунке. Он стартует из точки О в направлении, указанном стрелкой. На первом перекрёстке Петя поворачивает направо, на втором — налево, потом опять направо, потом опять налево, и так далее. В какой точке он не может оказаться?
(A) А (Б) Б (В) В (Г) Г (Д) Д
№8. Аня отметила на прямой линии 5 красных точек. В каждый промежуток между красными точками она поставила синюю точку, а потом в каждый промежуток между красной и синей точками — зелёную точку. Сколько всего точек получилось?
(A) 9 (Б) 15 (В) 17 (Г) 18 (Д) 20
№9. Аня, Боря, Вася, Гриша и Дима написали на доске числа 1, 3, 4, 6 и 8, каждый по одному числу. Васино число оказалось в 2 раза больше, чем Димино, а Борино — на 2 больше, чем Гришино. Какое число написала Аня?
(A) 8 (Б) 6 (В) 4 (Г) 3 (Д) 1
№10. Тысяча дециметров равна
(A) 10 км (Б) 1 км (В) 100 м (Г) 10 м (Д) 1 м
Задачи, оцениваемые в 4 балла
№11. С первого января 2015 года малыш Федя начал вести дневник. Он уверен, что в каждом месяце ровно 30 дней. Какую дату он напишет в своем дневнике 19 марта 2015 года в день конкурса «Кенгуру»?
(A) 17 марта (Б) 18 марта (В) 19 марта (Г) 20 марта (Д) 21 марта
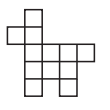
№12. Маша хочет разрезать по сторонам клеточек прямоугольник 4×3 так, чтобы из полученных частей можно было сложить фигурку, изображённую справа. На какое наименьшее число частей придётся разрезать прямоугольник?
(A) 2 (Б) 3 (В) 4 (Г) 5 (Д) 6
№13. Вася наклеил на лист бумаги одну за другой 5 круглых наклеек с цифрами. В каком
порядке он не мог их наклеивать?
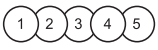
(A) 3, 2, 5, 4, 1 (Б) 5, 3, 4, 2, 1 (В) 3, 5, 1, 2, 4 (Г) 5, 3, 2, 4, 1 (Д) 3, 2, 1, 5, 4
№14. Друзья выясняли, какой сегодня день недели. Витя сказал: «Вчера было воскресенье». Сема сказал: «Завтра будет суббота». Петя сказал: «Позавчера была пятница». Саша сказал: «Послезавтра будет среда». Двое из них ошиблись. Какой сегодня день недели?
(A) понедельник (Б) вторник (В) среда (Г) четверг (Д) суббота
№15. Какой из результатов самый маленький?
 (A) (100 − 1) : 9 (Б) (1000 − 10) : 9 (В) (1000 − 1) : 9 (Г) (1000 − 100) : 9 (Д) (100 − 10) : 9
(A) (100 − 1) : 9 (Б) (1000 − 10) : 9 (В) (1000 − 1) : 9 (Г) (1000 − 100) : 9 (Д) (100 − 10) : 9
№16. Наташа рассматривает в лупу разные части рисунка на школьной доске. Какое из изображений А–Д она не сможет увидеть?

№17. Разность двух чисел на 3 меньше уменьшаемого и на 4 больше вычитаемого. Чему она равна?
(A) 7 (Б) 9 (В) 10 (Г) 12 (Д) 15
№18. Фигуру, изображённую на рис. 1, Вася разрезал на одинаковые треугольники, изображённые на рис. 2. Сколько треугольников у него получилось?
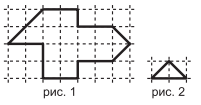
(A) 8 (Б) 12 (В) 14 (Г) 15 (Д) 16
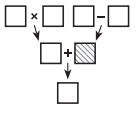
№19. Стрелочки на рисунке указывают на результаты действий с числами. Числа 1, 2, 3, 4, 5, 6 и 7 надо разместить по одному в квадратиках так, чтобы все результаты были правильными. Какое
число попадёт в заштрихованный квадратик?
(A) 1 (Б) 2 (В) 3 (Г) 4 (Д) 5
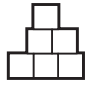
№20. Фигура на рисунке состоит из одинаковых квадратов со стороной 1 см. Чему равен её периметр?
(A) 9 см (Б) 10 см (В) 11 см (Г) 12 см (Д) невозможно определить
Задачи, оцениваемые в 5 баллов
№21. Маша заполняет горшочек крупой. Он будет полным, если в него насыпать 6 чайных ложек, 3 десертных и 1 столовую ложку крупы или 2 чайные ложки, 1 десертную и 3 столовые ложки той же крупы. У Маши есть только столовые ложки. Сколько таких ложек крупы ей придется насыпать?
 (A) 4 (Б) 5 (В) 6 (Г) 7 (Д) 8
(A) 4 (Б) 5 (В) 6 (Г) 7 (Д) 8
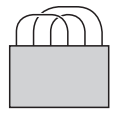
№22. У длинной верёвки связали концы и разложили получившуюся петлю на столе. Часть этой петли закрыта (смотри рисунок). Как может выглядеть закрытая часть?
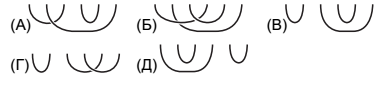
№23. В гостях у бабушки Женя и Лена ели мороженое ежедневно: каждая по 2 или 3 стаканчика. Всего Женя съела 25 стаканчиков, а Лена — 19. Сколько дней они гостили у бабушки?
(A) 8 (Б) 9 (В) 10 (Г) 11 (Д) 12

№24. В числовом ребусе буквами O, D, E, V, N обозначены разные цифры. Сколько различных цифр может обозначать буква V?
(A) 1 (Б) 2 (В) 3 (Г) 4 (Д) 5
№25. Дима, Федя, Надя и Катя пошли в лес за грибами. Известно, что Дима нашел грибов меньше, чем Федя, мальчики нашли грибов столько же, сколько девочки, а Дима и Надя нашли грибов больше, чем Федя и Катя. Кто нашел больше всех грибов?
(A) Дима (Б) Федя (В) Катя (Г) Надя (Д) невозможно определить
№26. Никита выписывает подряд целые числа 1, 2, 3,…, но он не любит цифру 7 и пропускает все числа, которые её содержат. Он выписал 777 чисел. Какое число он написал последним?
(A) 888 (Б) 1000 (В) 1053 (Г) 1333 (Д) 1631


