ЗАДАЧИ МЕЖДУНАРОДНОГО КОНКУРСА «Кенгуру»
17 марта 2016 г. 3–4 класс. Время, отведенное на решение задач, — 75 минут
Задачи, оцениваемые в 3 балла
№1. Кенга посмотрела на себя в зеркало. Что она увидела?
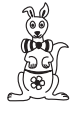
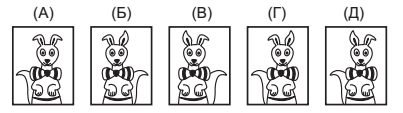
№2. Крошке Ру 17 марта исполняется 7 недель и 3 дня. Когда ему исполнится 9 недель?
(A) 21 марта (Б) 24 марта (В) 26 марта (Г) 28 марта (Д) 30 марта
№3. Какое число должно стоять в закрашенном квадратике?
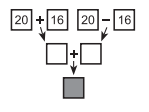
(A) 72 (Б) 56 (В) 40 (Г) 32 (Д) 20
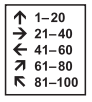
№4. Дима с папой пришли в цирк и ищут свои места с номерами 86 и 87. По какой стрелке им надо идти?

№5. Когда Саша зашифровала цифры буквами, оказалось, что 65832 = КЕНГА. Какое из следующих зашифрованных чисел самое маленькое?
(A) АГ (Б) ЕК (В) НЕ (Г) КА (Д) ГА
№6. Часть квадрата скрыта за шторкой. Какую форму имеет скрытая часть?
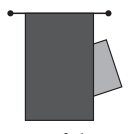
(А) треугольник (Б) четырехугольник (В) пятиугольник (Г) шестиугольник (Д) семиугольник
№7. Четвертое число в третьем десятке — это
(A) 43 (Б) 34 (В) 32 (Г) 24 (Д) 23
№8. Фигуры на рисунке — это круги, треугольники и квадраты. Что верно?
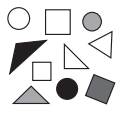
(A) Кругов больше, чем квадратов.
(Б) Квадратов больше, чем треугольников.
(В) Кругов в два раза больше, чем треугольников.
(Г) Треугольников в два раза больше, чем кругов.
(Д) Кругов меньше, чем треугольников.
№9. Значок весит 3 г. Сколько весит тысяча таких значков?
(A) 30г (Б) 300 г (В) 3 кг (Г) 30 кг (Д) 300 кг
№10. Среди этих четырех карточек есть две одинаковые. Какие?

(А) 1 и 4 (Б) 1 и 3 (В) 1 и 2 (Г) 2 и 3 (Д) 3 и 4
Задачи, оцениваемые в 4 балла
№11. Во дворе гуляют несколько собак. У этих собак лап на 18 больше, чем носов. Сколько собак во дворе?
(A) 4 (Б) 5 (В) 6 (Г) 8 (Д) 9
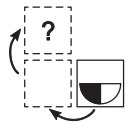
№12. Карточку, изображенную справа, перевернули сначала через левый край, а потом — через верхний край. Что получилось?

№13. Сумма двух чисел равна 170. Первое число оканчивается цифрой 5, а если эту цифру стереть, то получится второе число. Чему равна разность этих чисел?
(A) 110 (Б) 120 (В) 130 (Г) 140 (Д) 150
№14. Улитке нужно было проползти 12 метров. Утром до обеда она проползла 12 дм, а после обеда устала и проползла только 12 см. Какое расстояние ей осталось проползти?
(А) 1028 см (Б) 1068 см (В) 102 дм (Г) 10 м (Д) 11 м
№15. Когда число увеличили на 3, его последняя цифра уменьшилась. На сколько?
(А) на 7 (Б) на 6 (В) на 3 (Г) на 1 (Д) ответ зависит от числа
№16. В некотором году тринадцатое января было вторником. Каким числом в том же месяце был первый понедельник после первого вторника?
(A) 5 (Б) 7 (В) 12 (Г) 14 (Д) 19
№17. Крошка Ру хочет пройти из комнаты А в комнату В (см. рисунок). Через какое наименьшее количество дверей ему придется пройти?
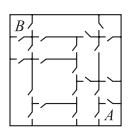
(A) 3 (Б) 4 (В) 5 (Г) 6 (Д) 7
№18. Самое маленькое из двузначных чисел с двузначной суммой цифр сложили с самым большим из двузначных чисел с однозначной суммой цифр. Что получилось?
(A) 90 (Б) 100 (В) 105 (Г) 109 (Д) 110
№19. На рисунке изображено пять стопок картонных карточек. В каждой стопке три карточки: треугольная, круглая и квадратная. В скольких стопках треугольная карточка лежит выше квадратной?

(A) 1 (Б) 2 (В) 3 (Г) 4 (Д) 5
№20. Каждую звездочку в примере 2*2*2 можно заменить на один из знаков арифметического действия. Какой результат нельзя получить?
(А) 1 (Б) 2 (В) 3 (Г) 6 (Д) все результаты А–Г можно получить
Задачи, оцениваемые в 5 баллов
№21. Электронные часы показывают часы и минуты. Например, в 6 часов утра они показывают 06:00, а в 6 часов вечера — 18:00. Сколько минут за сутки на табло часов будут видны ровно три нуля?
(A) 26 (Б) 25 (В) 24 (Г) 23 (Д) 12
№22. Пять различных точек А, В, С, D и Е расположены на прямой так, что АВ = 6, АD = 2, АЕ = 2, СЕ = 4. Какие две точки крайние?
(А) В и С (Б) С и D (В) А и D (Г) Е и D (Д) невозможно определить
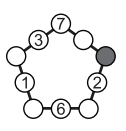
№23. Аня хочет вписать числа в пустые кружочки так, чтобы на всех сторонах пятиугольника суммы трех чисел были одинаковы. Какое число она должна вписать в закрашенный кружочек?
(A) 9 (Б) 10 (В) 13 (Г) 23 (Д) 40
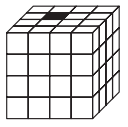
№24. Большой куб 4 ×4 ×4 сложен из 64 маленьких кубиков, один из которых красный, а остальные — белые (см. рисунок). По взмаху волшебной палочки каждый белый кубик, имеющий общую грань с красным кубиком, тоже становится красным. Сколько будет красных кубиков после трех взмахов волшебной палочки?
(A) 27 (Б) 32 (В) 33 (Г) 48 (Д) 64
№25. Два трехзначных числа составлены из шести различных цифр так, что первая цифра второго числа вдвое больше, чем последняя цифра первого числа. Какова наименьшая возможная сумма таких чисел?
(A) 597 (Б) 588 (В) 546 (Г) 537 (Д) 535
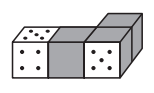
№26. Четыре одинаковых игральных кубика (общее число точек на противоположных гранях равно 7) приложили друг к другу одинаковыми гранями и закрасили некоторые грани (см. рисунок). Какое самое маленькое число точек могло быть закрашено на трех верхних гранях?
(A) 3 (Б) 4 (В) 5 (Г) 6 (Д) 7


