Задачи международного конкурса «Кенгуру»
16 марта 2017 г. 3–4 классы. Время, отведенное на решение задач — 75 минут!
Задачи, оцениваемые в 3 балла
№1. Кенга составила пять примеров на сложение. Какая сумма самая большая?
(А) 2+0+1+7 (Б) 2+0+17 (В) 20+17 (Г) 20+1+7 (Д) 201+7
№2. Ярик отметил стрелочками на схеме путь от дома до озера. Сколько стрелочек он нарисовал неправильно?

(А) 3 (Б) 4 (В) 5 (Г) 7 (Д) 10
№3. Число 100 увеличили в полтора раза, а результат уменьшили в два раза. Что получилось?
(А) 150 (Б) 100 (В) 75 (Г) 50 (Д) 25
№4. На рисунке слева изображены бусы. На каком рисунке изображены те же бусы?
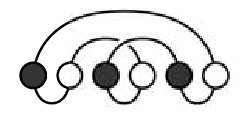
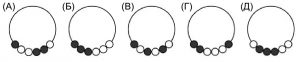
№5. Женя составила шесть трехзначных чисел из цифр 2,5 и 7 (цифры в каждом числе различны). Потом она расположила эти числа в порядке возрастания. Какое число оказалось третьим?
(А) 257 (Б) 527 (В) 572 (Г) 752 (Д) 725
№6. На рисунке изображены три квадрата, разбитых на клетки. На крайних квадратах часть клеток закрашена, а остальные – прозрачные. Оба эти квадрата наложили на средний квадрат так, что их верхние левые углы совпали. Какая из фигурок осталась видна?
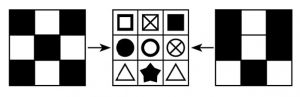
![]()
№7. Какое самое маленькое число белых клеток на рисунке надо закрасить, чтобы закрашенных клеток стало больше, чем белых?

(А) 1 (Б) 2 (В) 3 (Г) 4 (Д)5
№8. Маша нарисовала 30 геометрических фигур в таком порядке: треугольник, круг, квадрат, ромб, потом снова треугольник, круг, квадрат, ромб и так далее. Сколько треугольников нарисовала Маша?
(А) 5 (Б) 6 (В) 7 (Г) 8 (Д)9
№9. Спереди дом выглядит так, как изображено на рисунке слева. Сзади у этого дома есть дверь и два окна. Как он выглядит сзади?


№10. Сейчас 2017 год. Через сколько лет будет ближайший год, в записи которого нет цифры 0?
(А) 100 (Б) 95 (В) 94 (Г) 84 (Д)83
Задачи, оцениваемые в 4 балла
№11. Шарики продаются упаковками по 5, 10 или 25 штук в каждой. Аня хочет купить ровно 70 шариков. Какое самое маленькое число упаковок ей придется купить?
(А) 3 (Б) 4 (В) 5 (Г) 6 (Д) 7
№12. Миша сложил квадратный лист бумаги и проткнул в нём дырку. Потом он развернул лист и увидел то, что изображено на рисунке слева. Как могли выглядеть линии сгиба?
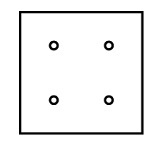

№13. Три черепахи сидят на дорожке в точках A, В и С (см. рисунок). Они решили собраться в одной точке и найти сумму пройденных ими расстояний. Какая самая маленькая сумма могла у них получиться?
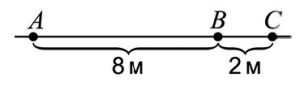 (А) 8 м (Б) 10 м (В) 12 м (Г) 13 м (Д) 18 м
(А) 8 м (Б) 10 м (В) 12 м (Г) 13 м (Д) 18 м
№14. В промежутки между цифрами 1 6 3 1 7 надо вставить два знака + и два знака × так, чтобы получился самый большой результат. Чему он равен?
(А) 16 (Б) 18 (В) 26 (Г) 28 (Д) 126
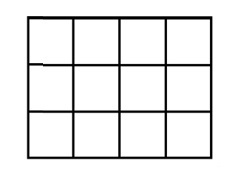
№15. Полоска на рисунке составлена из 10 квадратиков со стороной 1. Сколько таких же квадратиков надо приложить к ней справа, чтобы периметр полоски стал в два раза больше?
![]() (А) 9 (Б) 10 (В) 11 (Г) 12 (Д) 20
(А) 9 (Б) 10 (В) 11 (Г) 12 (Д) 20
№16. В клетчатом квадрате Саша отметила клетку. Оказалось, что в своем столбце эта клетка четвертая снизу и пятая сверху. Кроме того, в своей строке эта клетка шестая слева. Какая она справа?
(А) вторая (Б) третья (В) четвертая (Г) пятая (Д)шестая
№17. Из прямоугольника 4 × 3 Федя вырезал две одинаковые фигурки. Какого вида фигурки у него не могли получиться?

№18. Каждый из трех мальчиков загадал по два числа от 1 до 10. Все шесть чисел оказались различными. Сумма чисел у Андрея – 4, у Бори – 7, у Вити – 10. Тогда одно из Витиных чисел – это
(А) 1 (Б) 2 (В) 3 (Г) 5 (Д)6
№19. В клетках квадрата 4 × 4 расставлены числа. Соня нашла квадратик 2 × 2, в котором сумма чисел самая большая. Чему равна эта сумма?
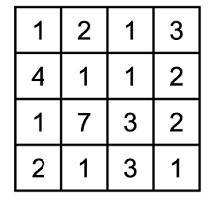 (А) 11 (Б) 12 (В) 13 (Г) 14 (Д) 15
(А) 11 (Б) 12 (В) 13 (Г) 14 (Д) 15
№20. Дима катался на велосипеде по дорожкам парка. Он въехал в парк в ворота А. Во время прогулки он три раза поворачивал направо, четыре раза налево и один раз разворачивался. Через какие ворота он выехал?
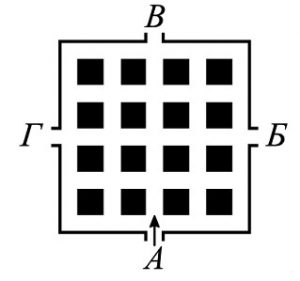
(А) А (Б) Б (В) В (Г) Г (Д) ответ зависит от порядка поворотов
Задачи, оцениваемые в 5 баллов
№21. В забеге участвовало несколько детей. Число прибежавших раньше Миши в три раза больше числа тех, кто прибежал после него. А число прибежавших раньше Саши в два раза меньше, чем число прибежавших после нее. Сколько детей могло участвовать в забеге?
(А) 21 (Б) 5 (В) 6 (Г) 7 (Д) 11
№22. В некоторых закрашенных клетках спрятано по одному цветочку. В каждой белой клетке написано количество клеток с цветочками, которые имеют с ней общую строну или вершину. Сколько цветочков спрятано?
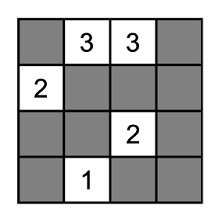 (А) 4 (Б) 5 (В) 6 (Г) 7 (Д) 11
(А) 4 (Б) 5 (В) 6 (Г) 7 (Д) 11
№23. Трехзначное число назовем удивительным, если среди шести цифр, которыми записывается оно и следующее за ним число, есть ровно три единицы и ровно одна девятка. Сколько всего удивительных чисел?
(А) 0 (Б) 1 (В) 2 (Г) 3 (Д) 4
№24.Каждая грань куба разделена на девять квадратиков (см. рисунок). Какое самое большое число квадратиков можно покрасить, чтобы никакие два покрашенных квадратика не имели общей стороны?
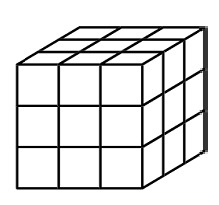 (А) 16 (Б) 18 (В) 20 (Г) 22 (Д) 30
(А) 16 (Б) 18 (В) 20 (Г) 22 (Д) 30
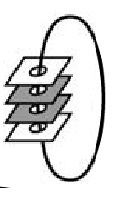
№25. Стопка карточек с дырками нанизана на нитку (см. рисунок слева). Каждая карточка с одной стороны белая, а с другой – закрашенная. Вася разложил карточки на столе. Что у него могло получиться?
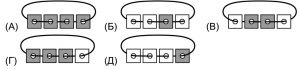
№26. Из аэропорта на автовокзал через каждые три минуты отправляется автобус, который едет 1 час. Через 2 минуты после отправления автобуса из аэропорта выехал автомобиль и ехал до автовокзала 35 минут. Сколько автобусов он обогнал?
(А) 12 (Б) 11 (В) 10 (Г) 8 (Д) 7


