Поступление в школу 2007
Вариант вступительного экзамена в 5 класс. 2020 год
Письменное собеседование
№1. Выполните действия в столбик:
а) 683594 + 28257; б) 576352 — 86924; в) 716 • 4307
№2. Выполните действия в столбик и поставьте знак >, < или в так, чтобы получилось верное равенство или неравенство:
424242 – 99144 : 243 ___ 355355 + 67489
№3. Решите по действиям: 4736 + (38962 : 14 – 230 • 7).
№4. Маша вырезала из бумаги прямоугольник и 2 квадрата. Длина прямоугольника равна стороне одного из квадратов, а ширина — стороне другого квадрата. Периметр меньшего из квадратов — 16 см. Сторона большого квадрата в 8 раз больше стороны маленького. Найдите периметр прямоугольника.
№5. В четырёх домах всего 1302 квартиры. В первом доме шестая часть от общего количества квартир. Во втором на 16 квартир больше, чем в первом. В четвертом в 2 раза меньше квартир, чем в третьем. Сколько квартир в третьем доме?
№6. Вычислите, покажите все промежуточные действия:
а) (39т 7ц 8кг) • 7 + 12 ц 4 кг;
б) (34 дм2 28мм2 -20см2 48мм2) • 5;
в) (15ч 29мин 57с + 2ч 30мин 43с) : 2.
№7. Вася в 8:00 вышел из дома и пошёл в гости к Пете со скоростью 35 м/мин. Петя живёт на расстоянии 820 м от Васи. Пройдя 350 м, Вася встретил хулигана Толю, и, не останавливаясь, побежал дальше, мгновенно увеличив свою скорость до 94 м/мин. Толя не сразу сообразил, что происходит, и стал догонять Васю лишь через минуту после их встречи. Бежал Толя со скоростью 117 м/мин.
а) В какое время Вася прибежал в гости к Пете?
б) На каком расстоянии от Васи находился Толя, когда Вася добрался до дома Пети?
№8. Юля задумала число и уменьшила его в 3 раза. Результат увеличила на самое маленькое двузначное число. Полученное число уменьшила в 4 раза. Разделила 420 на результат. От полученного числа отняла 25 и получила 45. Какое число задумала Юля?
№9. В равенстве (2174* +4): (225 : 3) = *** некоторые цифры заменили на звездочки.
Восстановите равенство, и сделайте проверку (приведите вычисления по действиям).
№10. Для посадки моркови закупили роботов. Все роботы сажают морковь с одинаковой постоянной скоростью. Три робота, работая вместе, могут посадить 360 морковок за 4 часа.
а) За какое время один робот сажает одну морковку?
б) Сколько нужно роботов, чтобы посадить за 6 часов 1260 морковок?
№11. В оконный проём вставлена рама (закрашена), которая сделана из досок с шириной 1 дм. В
раму вставлены три стекла: одно прямоугольное с длиной 13 дм и два одинаковых квадратных. Площадь оконного проёма 270 дм2. Найдите:
а) периметр оконного проёма;
б) площадь прямоугольного стекла.
Устное собеседование
№1. В коробке лежат синие, красные и зелёные карандаши. Всего 20 штук. Синих в 6 раз больше, чем зеленых. Красных меньше чем синих. Сколько в коробке карандашей каждого цвета?
№2. У Малыша есть конфеты, несколько коробок и ящичек. Каждое утро Малыш высыпает все конфеты на ковёр и раскладывает по-новому. В понедельник он положил в ящичек 6 конфет, а оставшиеся удалось поровну разложить в 6 коробок. Во вторник Малыш положил в ящичек 9 конфет, а оставшиеся удалось поровну разложить в 9 коробок. В среду в ящичке было 17 конфет, а оставшиеся удалось разложить поровну в 17 коробок. Сколько конфет может быть у Малыша? (Достаточно придумать один пример.)
№3. В миске лежали орешки. Маша съела половину всех орешков и ещё два. Потом Катя положила в карман 6 орешков и съела половину того, что осталось. Затем Витя съел треть того, что осталось. После этого Денис съел четверть остатка, а Катя высыпала в миску орешки из кармана. В миске стало 24 орешка. Сколько орешков было в начале? Сколько орешков съел каждый?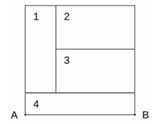
№4. Квадрат разрезан на четыре прямоугольника равной площади (см. рис.). Найдите периметр прямоугольника №2, если АВ = 96см.
№5. Лиса и два медвежонка делят 120 конфет. Лиса раскладывает конфеты на три кучки, затем жребий определяет, кому какая достанется. Лиса знает, что если медвежатам достанется разное количество конфет, то медвежонок, у которого кучка будет больше, отдаст лишние конфеты ей. После этого все едят доставшиеся им конфеты. Может ли Лиса так разложить конфеты, чтобы гарантированно съесть больше 80, но не больше 85, если среди кучек не должно быть одинаковых? Если может, покажите, как, если не может, объясните, почему.
