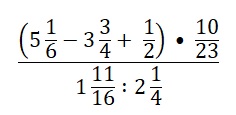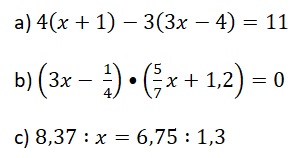Поступление в школу 2007

Вариант вступительного экзамена в 7 класс. 2020 год

Письменное собеседование

№1. Вычислите, написав все промежуточные вычисления:

№2. Решите уравнения:

№3. Рюкзак Васи весит 12 кг. Вес учебников составляет 72% веса рюкзака. А тетради – 2/3 оставшегося веса. Пенал весит столько же, как и пустой рюкзак. Сколько весят учебники? Сколько весят тетради? Сколько весит пенал?

№4. Между домами Алика и Бори 18 км. Мальчики одновременно выбежали навстречу друг другу. Алик бежал со скоростью 7 км/ч, а Боря – со скоростью 2 км/ч. Через 20 минут после их старта выбежала собака одного из мальчиков и побежала за хозяином со скоростью 40 м/мин. Известно , что собака и мальчики встретились одновременно. Кому из мальчиков принадлежит собака?

№5. Масса куска сплава Вибраниума и Адамантия составляет 1440 граммов. Масса Адамантия в сплаве в 5 раз больше, чем масса Вибраниума. Сколько граммов Адамантия нужно добавить, чтобы Вибраниум составлял 15% от массы  нового сплава?

№6. Три мальчика собирали грибы. Вес грибов, собранных Антоном и Борей, соотносятся как 5,4 : 3,6. А Ваня собрал 2/5 того веса, что собрал Антон. Сколько килограммов грибов собрал каждый из мальчиков, если Боря собрал на 1,6 кг больше, чем Ваня?

№7. В числе 3151*26* две цифры заменили на звездочки. Найдите исходное число, если известно, что оно делится на 36. Найдите все возможные варианты ответа и докажите, что других нет.

Устное собеседование

№1. Женя купила конфеты. Сначала она съела 1/4 всех конфет и еще 2 конфеты, потом — 1/4 остатка и еще 1 конфету. Сколько конфет было у Жени сначала, если у нее осталось не менее 13 и не более 21 конфеты?

№2. Вася упаковывает яблоки. Если он кладет по 5 штук в коробку, то останется 1 яблоко, если по 3 штуки – то 2 яблока, а если по 4 штуки в коробку – то остатка не остается. Какое количество яблок могло быть у Васи, если у него было не менее 600 и не более 800 штук?

№3. В какой пропорции нужно смешать 11-процентный и 23-процентный растворы йода, чтобы получить 19-процентный раствор?

№4. На доске написаны числа 1, 2, 3, 4, 5, 6. За один ход разрешается прибавить к любым двум числам по 1. Можно ли за несколько ходов сравнять эти числа?

№5. Один путник прошел первую половину пути со скоростью 4 км/ч, а вторую половину пути – со скоростью 5 км/ч. Другой шел половину времени своего путешествия со скоростью 4 км/ч, а вторую половину времени – со скоростью 5 км/ч. С какой постоянной скоростью должен идти каждый из них, чтобы пройти этот путь за то же самое время?