Поступление в Школу «Интеллектуал»
Вариант вступительного экзамена в 5 класс. 2018 год
Математика базовый
№1. (1,5 балла) Найдите значение выражения: 76+(165 − 9 ∙ 15):15
№2. (1,5 балла) 4 ч 15 мин равны a) 24900 сек b) 1530 сек c) 14700 сек d) 15300 сек e) 25500 сек
№3. (3 балла) Дан ряд чисел. 13530; 7365; 67; 20360; 3315; 100000; 136; 3732; 932. Выберите все верные утверждения:
a) Среди чисел в этом ряду ровно четыре числа делятся на 5 без остатка.
b) Если самое маленькое число из этого ряда поделить на 6, то остаток будет равен 7.
c) Разность самого большого и самого маленького числа из этого ряда является пятизначным числом.
d) В этом ряду количество четырёхзначных чисел равно количеству нечётных чисел.
e) Ровно у двух чисел в этом ряду в разряде сотен стоит тройка.
№4. (1,5 балла) В магазине спортивной одежды две футболки и три кепки стόят 195 долларов. Две кепки и футболка стόят 105 долларов. Сколько стоит футболка вместе с кепкой?
№5. (1,5 балла) Среднюю скорость можно вычислить, если поделить весь пройденный путь на всё время, затраченное на этот путь. Богатырь Добрыня на своём Коне проскакал три часа со скоростью 16 вёрст в час, а потом ещё час – со скоростью 12 вёрст в час. Найдите среднюю скорость богатырского Коня.
№6. (4 балла) Робот Виталий получил задание: он должен покрыть прямоугольный лист металла размером 200 см х 300 см одинаковыми пластиковыми квадратами размером 2 дм х 2 дм так, чтобы весь лист был покрыт без нахлёстов и дырок. При этом в центр каждого квадрата и во все места, где соединяются вершины четырёх квадратов, робот Виталий приделывает заклёпку. Сколько заклёпок ему понадобится?
№7. (3 балла) Для покраски поверхности площадью 1 дм2 требуется 20 граммов краски. Для того, чтобы покрасить кубики с длиной ребра 3 дм, ученики пятого класса купили каждый по банке с краской. Кому из них хватит краски для того, чтобы покрасить свой кубик целиком, если:
- a) Петя купил банку, в которой 360 грамм краски.
- b) Вася купил банку, в которой 540 грамм краски.
- c) Петя купил банку, в которой 1080 грамм краски.
- d) Коля купил банку, в которой 180 грамм краски.
- e) Миша купил банку, в которой 1200 грамм краски.
Выберите все успешные варианты.
№8. (4 балла) В Маленьком театре есть 20 рядов кресел для зрителей, по 8 кресел в каждом ряду. В партере помещаются ряды с 1-го по 4-й; на балконе – четверть оставшихся; остальные ряды – это амфитеатр. Выберите все неверные утверждения:
a) На балконе на 8 мест больше, чем в партере.
b) В амфитеатре расположена ровно половина всех кресел для зрителей.
c) В партере на четыре ряда кресел меньше, чем в амфитеатре.
d) В амфитеатре на 64 кресла больше, чем на балконе.
e) На балконе и в партере в сумме 72 места.
Математика по выбору
№1. Автомат делит чётное число пополам, а к нечётному прибавляет 5. Известно, что за три шага автомат получил из натурального нечетного числа N число 5. Найдите сумму цифр числа N.
№2. Чему равно выражение 10000 • AROO–10000 • KANG + KANGAROO, если разные буквы изображают разные цифры? Обведите правильный ответ:
(1) AROOAROO (2) AROOKANG (3) KANGKANG
(4) KANGAROO (5) ARKANGOO
№3. Пять джентльменов: A, B, C, D и E встретились в клубе. Некоторые из них приветствовали друг друга рукопожатиями. При этом А и В пожали руку по одному разу, а С, D и Е – по два. Известно, что А пожал руку Е. Какого рукопожатия точно не было? Обведите правильный ответ.
Ответ: (1) C – D (2) C – E (3) B – Е (4) B – D (5) B – С
№4. Целые числа от 1 до 7 вписывают по одному в кружки на рисунке так, чтобы суммы чисел в каждой тройке кружков, расположенных на прямой линии, были одинаковыми, а цифры в кружках не повторялись. Запишите ВСЕ возможные цифры (или цифру), которые могут стоять в центральном кружке.
№5. В прямоугольнике размером 300х200 клеток, нарисованном на клетчатой бумаге, провели диагональ. Сколько клеточек она разрезала?
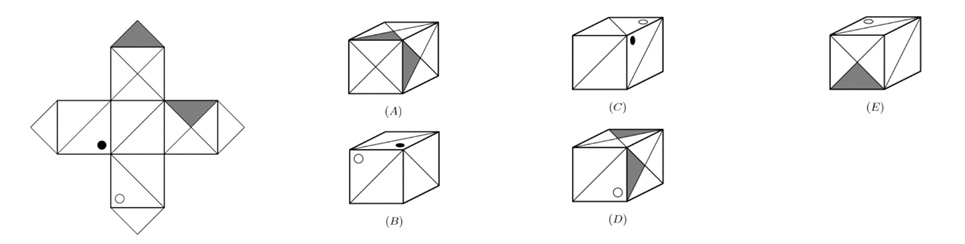
№6. Один из нарисованных кубиков не может иметь развёртки, изображенной на левом рисунке. Какой? В ответе укажите соответствующую букву.
№7. В одном австралийском городе на площади стоит памятник Кенгуру. К этой площади ведёт шесть улиц. По четырём из них разрешено двустороннее движение, а по двум – одностороннее, по направлению к площади. Турист на автомобиле собирается приехать на площадь, посмотреть памятник, а затем покинуть площадь. Сколько различных маршрутов он может для этого построить?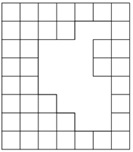
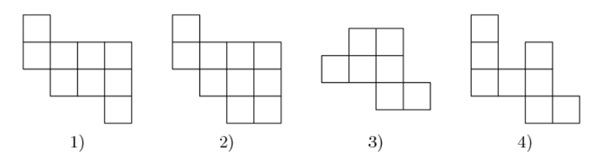
№8. Из листа клетчатой бумаги вырезали два кусочка. В результате образовалась дыра, изображенная на рисунке. Найдите вырезанные кусочки среди фигур 1) — 4).
а) Нарисуйте, как они располагались в дыре, заштриховав их так, чтобы кусочки отличались;
б) В ответе укажите номера нужных кусочков.
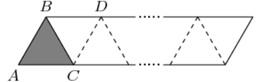
№9. На столе лежит длинная полоска бумаги, разделенная линиями на 2000 одинаковых равносторонних треугольников. Правый край полоски закреплён. Полоску надо сложить по всем этим линиям, «наматывая» на треугольник АВС. Сначала полоску сгибаем по линии ВС так, чтобы точка A наложилась сверху на точку D, затем сгибаем по линии CD так, чтобы уже сложенная часть оказалась сверху оставшейся полосы, и т. д. В каком положении окажутся точки А, В и С после 1999 шагов?
Обведите правильный ответ.
№10. Король хочет построить шесть крепостей и соединить каждые две из них дорогой, не проходящей через другие крепости (всего 15 дорог). Нарисуйте такую схему расположения крепостей и дорог, чтобы на ней было только три перекрестка и на каждом из них пересекались ровно две дороги:
Крепости на схеме можно обозначить кружочками.
Ответом является нарисованная здесь схема.