Всероссийская олимпиада школьников

Демонстрационный вариант 2016–2017 уч. г. ШКОЛЬНЫЙ ЭТАП. 4 КЛАСС

№1. (7 баллов) Замените звёздочки цифрами так, чтобы равенство стало верным и все семь цифр были различными: ** + ** = 175.

№2. (7 баллов) В Солнечном городе меняют пряник на 6 сушек, а за 9 сушек дают 4 баранки. Сколько баранок дают за 3 пряника? Объясните свой ответ.

№3. (7 баллов) Проведите два отрезка с концами на сторонах треугольника так, чтобы треугольник оказался разбит на два треугольника, один четырёхугольник и один пятиугольник.

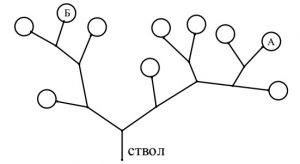
№4. (7 баллов) Чтобы добраться от ствола к любому листу дерева, изображённого на рисунке, нужно на каждой развилке повернуть либо налево, либо направо. Например, для того чтобы добраться до листа с буквой А, нужно пройти так: ппплп (буква п — это поворот на развилке вправо, буква л — поворот влево).

1. Напишите с помощью букв п и л путь к листу Б.
2. Дорисуйте на этом дереве ещё один лист так, чтобы на получившемся дереве был лист, соответствующий такому пути: пплплл. Напишите в листе, к которому ведет путь пплплл, букву В.

№5. (7 баллов) У Вани, Тани и Оли есть 12 одинаковых по форме шариков: несколько жёлтых, несколько синих и несколько красных. Они разложили шарики по 4 штуки в три одинаковых пакета. Ваня сказал: «Смотрите, ни в одном пакете нет трёх одинаковых шариков!» Таня сказала: «Верно. Но и трёх разных шариков тоже нет ни в одном пакете!» Оля сказала: «И все пакеты получились разными!». Все трое были правы. Обязательно ли в каком-то пакете лежит два жёлтых и два красных шарика? Объясните подробно свой ответ.

Максимальный балл за все выполненные задания — 35